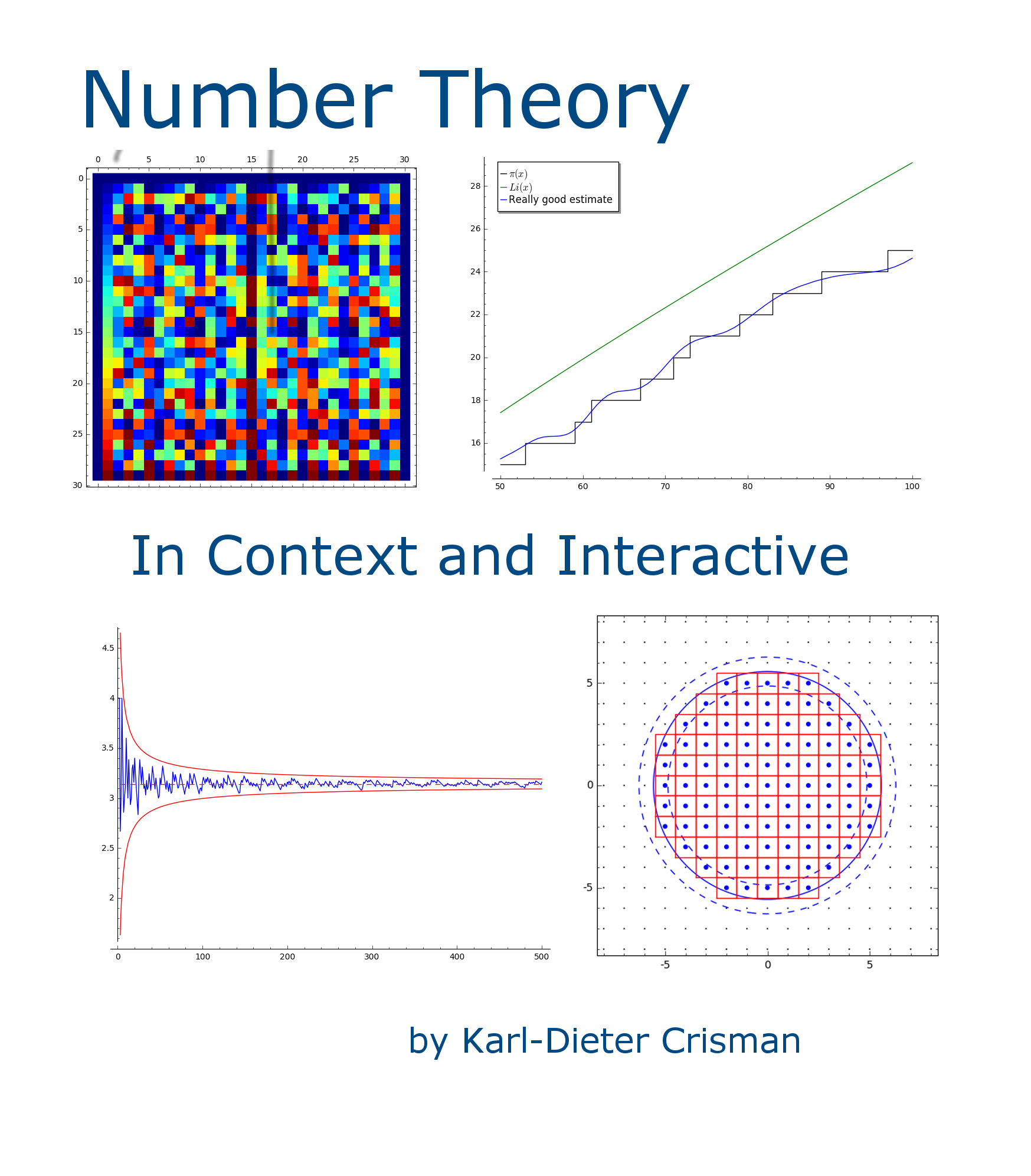
Section 10.1 Primitive Roots
Subsection 10.1.1 Definition
Definition 10.1.1.
We say that \(a\in U_n\) is a primitive root of \(n\) when \(a^b\) runs through all elements of \(U_n\) for \(1\leq b\leq \phi(n)\text{.}\)
Or, you can say the row corresponding to a primitive root hits all the possible colors in the visualization! For composite \(n\text{,}\) this won't mean all colors per se, just all colors that represent units. (See the colorbar below.) So for such moduli, we shrink the number of rows down for this visualization; it has rows only for the elements of \(U_n\text{.}\)
By the way, can you ‘see’ Euler's Theorem in this graphic? (Don't forget that it generalizes Fermat's Little Theorem.) Try exploring it in the interact as well, which allows not just for prime moduli but composite ones as well.

Sage note 10.1.3. Filtering list comprehensions.
We are only looking at units here. Where does this show up in the code? The syntax [x for y in range(1,mod) if func(x)] takes list comprehensions to another level, by ‘filtering’. This allows us to remove from the list anything which doesn't fit what we want. In this case, we removed non-units; gcd(a,mod)==1 was required.
Subsection 10.1.2 Two characterizations
Proposition 10.1.4.
There are two equivalent ways to characterize/define a primitive root of \(n\) among numbers such that \(\gcd(a,n)=1\text{.}\)
We say that \(a\) is a primitive root of \(n\) if \(a^b\) yields every element of \(U_n\text{.}\)
We say that \(a\) is a primitive root of \(n\) if the order of \(a\) is \(\phi(n)\text{.}\)
Proof.
Why are these true? Recalling the terminology from Section 8.3, the first one means that \(U_n\) is a cyclic group (one all of whose elements are powers of a specific element), and that \(a\) is a generator of that group. This is the more advanced point of view.
The second point of view also uses the group idea of the order of an element. Remember, this is the smallest number of times you can multiply something by itself and get 1 as a result. What would this idea mean without using the terminology of groups? With that viewpoint, \(k\) is the order of \(a\) if \(a^k\equiv 1\) (mod \(n\)) and \(a^b\not \equiv 1\) for \(1\leq b<k\text{.}\)
Subsection 10.1.3 Finding primitive roots
As a first exercise, the gentle reader should figure out the orders of some elements of some small groups of units. For \(n\in \{5,7,8,9,10,12,14,15\}\text{,}\) try exploring \(U_n\text{.}\) There should be at least some primitive roots.
Question 10.1.5.
In exploring \(U_n\) for some \(n\in \{5,7,8,9,10,12,14,15\}\text{:}\)
Were all elements primitive roots?
Did all of these groups have primitive roots?
Is it particularly fun to look for them?
It's useful to try looking for primitive roots by hand. However, it's better to know whether one should bother to look, and hence to try to prove things about orders in general.